I 1952 snudde en 24 år gammel student, Harry Markowitz, finansindustrien på hodet.
Han mente at investorer og forvaltere fokuserte for mye på avkastning og risiko til individuelle aksjer i porteføljen. Etter Markowitz’ mening var det viktigere å se på hvordan individuelle aksjer påvirket porteføljens samlede avkastning og risiko.
Hans artikkel “Portfolio Selection” blir sett på som finansindustriens Big Bang. Akkurat som når menneskene først lærte å bruke ild, var dette når investorer først lærte å bygge skikkelige porteføljer. Takket være en 24-åring. I 1990 ble han tildelt Nobelprisen i økonomi for hans banebrytende arbeid.
A good portfolio is more than a long list of good stocks and bonds. It is a balanced whole, providing the investor with protections and opportunities with respect to a wide range of contingencies. – Harry Markowitz, 1952

Hva er Moderne Porteføljeteori (MPT)
Moderne porteføljeteori (MPT) er en matematisk modell som forklarer hvordan investorer kan diversifisere porteføljen sin for å oppnå best risikojustert avkastning. Teorien hevder at for hvert nivå av risiko finnes det en optimal portefølje som maksimerer forventet avkastning (eller motsatt, at hvor hvert nivå av forventet avkastning finnes det en optimal portefølje som minimerer risikoen).
Begrepet “optimal portefølje” henviser til alle porteføljer som gir best risikojustert avkastning for hvert nivå av risiko. Det er jo uendelig mange måter å sette sammen en portefølje, for eksempel en med 10 aksjer, men bare én av de gir best risikojustert avkastning.
Han kalte alle optimale porteføljer for effisient fronten, mer om den straks.
Diversifisering er et viktig konsept. Markowitz hevdet med moderne porteføljeteori at det er mulig å oppnå bedre risikojustert avkastning ved å diversifisere smart, enn om man diversifiserte vilkårlig.
Se på porteføljens samlede risiko
Markowitz’ viktigste bidrag til verden av kapitalforvaltning er etter min mening hans syn på risiko og avkastning i en portefølje.
For frem til 1952 var det i stor grad tommelfingerregler som styrte porteføljeforvaltningen, ifølge Nobelprisvinner Myron S. Scholes, kjent for å ha utviklet Black-Scholes-formelen.
It was all rules of thumb. Nothing. He was developing things in a vacuum.… The Big Bang Theory in finance really occurred in 1952. – (Fabozzi, Jacobs, & Levy, 2024, s. 2).
Han forklarte at det ikke er risikoen til individuelle investeringer som er viktig når man bygger en portefølje, men hvordan en investering påvirker den samlede risikoen til porteføljen hvis den legges til. Korrelasjonen mellom investeringene i porteføljen er avgjørende.
Vil du lære aksjeanalyse? Da er nettkurset Fundamental analyse av aksjer: Finn fantastiske selskaper perfekt for deg. Lær hvordan profesjonelle investorer analyserer aksjer og finner de beste investeringene.
Antagelser i Moderne Porteføljeteori
Moderne porteføljeteori (MPT) er nettopp det – en teori. Den bygger på en rekke antagelser som ikke er helt forenelig med virkeligheten. For eksempel:
- Investorer er rasjonelle og prøver å maksimere avkastning for et gitt risikonivå.
- Investorer er risikoaverse, noe som betyr at de foretrekker lavere risiko for samme nivå av forventet avkastning.
- Investorer har de samme forventningene til avkastning, risiko og korrelasjon mellom investeringer.
- Markedet er sterkt effisient, investorer har tilgang til den samme informasjonen og det er ingen transaksjonskostnader.
- Avkastning er normalfordelt.
Investorer er ofte irrasjonelle, har ulike mål, og vurderer risiko og avkastning på forskjellige måter. Markedet er heller ikke perfekt effisient, og avkastning i aksjemarkedet har vist seg å være lognormalfordelt snarere enn normalfordelt; det er større sjanse for positive og negative outliers og fat tails – ekstreme hendelser. Investorer har ikke den samme informasjonen heller.
Likevel har MPT stor verdi. Teorien gir oss en ramme for å forstå hvordan diversifisering kan redusere risiko og hvordan investeringer bør vurderes i sammenheng med hele porteføljen, ikke isolert.
Hvordan bruke Moderne Porteføljeteori
Modellen antar at hvis en investor kan velge mellom to porteføljer med samme forventet avkastning, så vil investoren velge den minst risikable. La oss nå se på matematikken bak dette, og hvordan den brukes for å finne optimale porteføljer.
For å klare dette må vi regne ut to ting:
- Forventet avkastning for en portefølje
- Forventet risiko for en portefølje
Forventet avkastning for en portefølje
Forventet avkastning for en portefølje er den vektede gjennomsnittlige avkastningen av de enkelte investeringene i porteføljen, der vektene representerer andelen av hver investering i porteføljen.
FORMEL: Porteføljens forventede avkastning
\[ E(R_p) = \sum_{i=1}^N w_i E(R_i) \]La meg vise denne utregningen med et eksempel. La oss si vi har to aksjer med følgende egenskaper:
| Navn | Forventet avkastning | Allokering |
| Aksje 1 | 10% | 40% |
| Aksje 2 | 13% | 60% |
UTREGNING: Porteføljens forventede avkastning
(0,1*0,4) + (0,13*0,6) = 11,8%
Vi tar altså bare aksjens vekt i porteføljen multiplisert med dens forventede avkastning, og summerer opp dette.
Forventet risiko for en portefølje
Modellen måler risiko med standardavvik. Men sammenlignet med måten vi beregnet forventet avkastning, så kan vi ikke kalkulere forventet risiko ved å ta summen av det vektede standardavviket til de enkelte investeringene.
Vi må ta med i beregningen hvordan investeringene beveger seg i forhold til hverandre! Dette var den store innsikten til Markowitz. Korrelasjonen mellom investeringene må altså med for å beregne porteføljens samlede risiko. Beregningen blir derfor hakket mer avansert.
Standardavviket til porteføljen avhenger altså av (1) standardavviket til de individuelle aksjene, (2) allokeringen av kapital på aksjene og (3) korrelasjonen mellom alle aksjene – kjent som korrelasjonskoeffisienten.
FORMEL: Porteføljens standardavvik
\[\sigma_p = \sqrt{\sum_{i=1}^N \sum_{j=1}^N w_i w_j \sigma_i \sigma_j \rho_{ij}}\]- \( \sigma_p \): Porteføljens standardavvik
- \( w_i, w_j \): Vekten til aksje \( i \) og aksje \( j \) i porteføljen
- \( \sigma_i, \sigma_j \): Standardavviket (risikoen) for aksje \( i \) og aksje \( j \)
- \( \rho_{ij} \): Korrelasjonen mellom avkastningen til aksje \( i \) og aksje \( j \)
- \( N \): Antall aksjer i porteføljen
Hvis vi har en portefølje med kun to aksjer, blir utregningen slik:
FORMEL: Porteføljens standardavvik med to aksjer
\[\sigma_p = \sqrt{w_1^2 \sigma_1^2 + w_2^2 \sigma_2^2 + 2 w_1 w_2 \sigma_1 \sigma_2 \rho_{12}}\]- \( \sigma_p \): Porteføljens standardavvik
- \( w_1, w_2 \): Vekten til aksje 1 og aksje 2 i porteføljen
- \( \sigma_1, \sigma_2 \): Standardavviket for aksje 1 og aksje 2
- \( \rho_{12} \): Korrelasjonen mellom aksje 1 og aksje 2
La oss nå si vi har følgende tall for våre aksjer:
| Aksje | Varians | Standardavvik | Korrelasjon | Fordeling |
| Aksje 1 | 1% | 10% | 0,3 | 40% |
| Aksje 2 | 2,25% | 15% | 0,3 | 60% |
UTREGNING: Porteføljens standardavvik med to aksjer
- For aksje 1: \( w_1^2 \sigma_1^2 = 0.0016 \)
- For aksje 2: \( w_2^2 \sigma_2^2 = 0.0081 \)
- Kryssledd: \( 2 w_1 w_2 \sigma_1 \sigma_2 \rho_{12} = 0.00216 \)
- Totalt: \( \sigma_p^2 = 0.0016 + 0.0081 + 0.00216 = 0.01186 \)
- Porteføljens standardavvik: \( \sigma_p = \sqrt{0.01186} \approx 0.109 \) eller 10,9%
Legg merke til at jeg kaller de for forventet avkastning og forventet risiko, men baserer denne forventningen på historiske tall. Det er ingen garanti for at historien gjentar seg. I tillegg er det problematisk å måle risiko med standardavvik, da det kun er en representasjon for reell risiko: sannsynligheten for tap av kapital.
For å beregne risikojustert avkastning kan vi eksempelvis bruke Sharpe Ratio:
UTREGNING: Porteføljens risikojusterte avkastning målt med Sharpe Ratio
(11,8 – 4,22)/10,9 = 0,69
I skrivende stund er risikofri rente 4,22%.
I en portefølje med mange aksjer og andre investeringer, blir spørsmålet hvilken kombinasjon av aksjene som gir best risikojusterte avkastningen.
Her kommer konseptet om effisient fronten inn.
Liker du utbytteaksjer? I nettkurset Utbytteaksjer: Bygg formue med en solid utbytteportefølje lærer du å finne solide utbytteaksjer som betaler utbytte i lang tid.
Effisient Fronten: Alle optimale porteføljer
Effisient fronten er et konsept i moderne porteføljeteori som henviser til alle varianter av en portefølje (for eksempel en portefølje med tre aksjer) som er optimalt konstruert i forhold til risiko og avkastning.
Den representerer alle porteføljer som gir høyest forventet avkastning for et gitt risikonivå (eller lavest risiko for en gitt forventet avkastning) – disse porteføljene kalles for “optimale porteføljer”.
Effisient fronten blir illustrert med en linje som lages ved å trekke en strek gjennom alle optimale porteføljer. Hver prikk representerer en mulig portefølje, og kun de som ligger på effisient fronten gir best risikojustert avkastning.
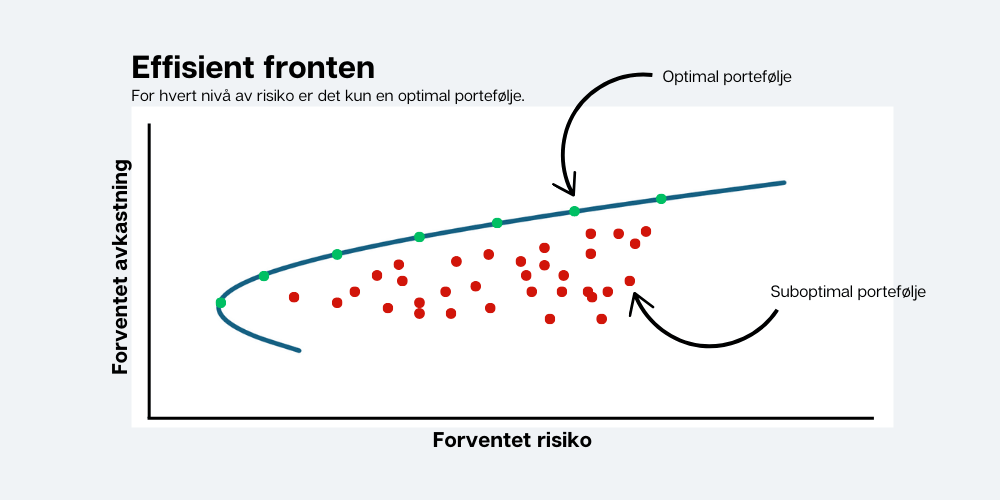
Tenk deg nå at bildet over illustrerer alle mulige kombinasjoner av en porteføljen med 15 aksjer. De aller fleste vil være suboptimale – de vil gi dårligere risikojustert avkastning for et gitt risikonivå (eller for et gitt avkastningsnivå). Noen vil derimot være optimale og være en del av effisient fronten.
Hvordan finner vi de optimale porteføljene? Dette er et matematisk optimeringsproblem, men jeg er ikke et mattegeni og har ikke tenkt til å finne frem penn og kalkulator for å finne svaret. I praksis brukes regnearkprogrammet Excel til å gjøre kompliserte beregninger for å finne svaret.
Det sparer vi til en annen artikkel!
Moderne porteføljeteori er ikke bare en samling formler og konsepter; det er en måte å tenke på som har forandret hvordan vi bygger og forvalter investeringer. Jeg synes det er utrolig inspirerende at en 24 åring fikk til dette. Fra å fokusere på enkeltselskaper til å se porteføljen som en helhet, introduserte Markowitz oss for et paradigmeskifte som har stått stødig i over 70 år.
Som Markowitz så treffende sa: En god portefølje er mer enn en liste over gode aksjer og obligasjoner. Det er en balansert helhet.
Vanlige spørsmål om Moderne Porteføljeteori
Moderne porteføljeteori, utviklet av Harry Markowitz, er en matematisk modell som fokuserer på å maksimere avkastning for en gitt risikonivå eller minimere risiko for en gitt avkastning. Modellen bygger på diversifisering og korrelasjon mellom investeringer.
Den effisiente fronten er en grafisk representasjon av porteføljer som gir høyest mulig avkastning for et gitt risikonivå. Den hjelper investorer med å identifisere optimale porteføljer basert på deres risikotoleranse. I praksis beregnes den med regnearkprogram som Excel.
I moderne porteføljeteori måles risiko vanligvis ved standardavviket til porteføljens avkastning. Standardavvik reflekterer hvor mye avkastningen svinger rundt gjennomsnittet sitt. Hovedpoenget til Markowitz var at korrelasjonen mellom investeringer reduserer den samlede risikoen til porteføljen.











